Kí hiệu. 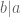 nghĩa là
nghĩa là  chia hết cho
chia hết cho 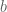 , còn
, còn 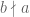 nghĩa là
nghĩa là  không chia hết cho
không chia hết cho 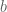 .
.
Định nghĩa. Cho 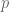 là số nguyên tố,
là số nguyên tố,  là số nguyên và
là số nguyên và 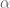 là số tự nhiên. Ta có
là số tự nhiên. Ta có 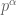 là lũy thừa đúng (exact power) của
là lũy thừa đúng (exact power) của  và
và 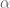 là số mũ đúng (exact exponent) của
là số mũ đúng (exact exponent) của 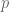 trong khai triển của
trong khai triển của  nếu
nếu 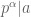 và
và 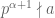 . Khi đó ta viết
. Khi đó ta viết 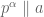 hay
hay 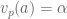 .
.
Ví dụ. Ta có 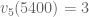 vì
vì 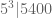 và
và 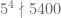 .
.
Tính chất. Với 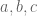 là các số nguyên,
là các số nguyên, 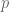 là số nguyên tố thì:
là số nguyên tố thì:
.
.
. Dấu đẳng thức xảy ra khi
.
.
.
II. Định lí về số mũ đúng (LTE)
Cho 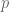 là số nguyên tố,
là số nguyên tố, 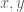 là hai số nguyên không chia hết cho
là hai số nguyên không chia hết cho 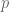 . Khi đó
. Khi đó
a) Với mọi số nguyên dương 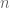 thì
thì
- Nếu
và
thì
.
- Nếu
và
thì
.
- Nếu
và
,
chẵn thì
.
b) Nếu 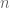 là số nguyên dương lẻ, nếu
là số nguyên dương lẻ, nếu 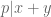 thì
thì 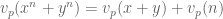 .
.
Chú ý. Để chứng minh 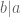 thì ta cần chứng minh
thì ta cần chứng minh 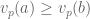 với
với 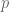 là ước nguyên tố của
là ước nguyên tố của 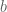 . Hay nói cách khác,
. Hay nói cách khác, 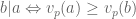 .
.
III. Một số ví dụ
Ví dụ 1. Cho 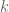 là số nguyên dương. Tìm mọi số nguyên dương
là số nguyên dương. Tìm mọi số nguyên dương 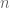 thỏa mãn
thỏa mãn 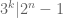 .
.
Lời giải. Với 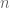 lẻ thì
lẻ thì 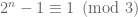 nên không thể chia hết cho
nên không thể chia hết cho 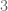 , trường hợp này loại.
, trường hợp này loại.
Với 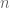 chẵn thì đặt
chẵn thì đặt 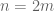 với
với 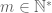 . Khi đó
. Khi đó 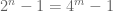 . Áp dụng bổ đề LTE ta có
. Áp dụng bổ đề LTE ta có 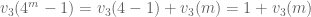 . Để
. Để 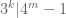 thì
thì 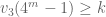 hay
hay 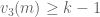 . Do đó
. Do đó 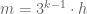 với
với 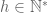 .
.
Vậy 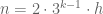 với
với 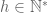 .
.
Ví dụ 2. (UNESCO Competition 1995) Cho 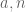 là hai số nguyên dương và cho
là hai số nguyên dương và cho 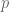 là số nguyên tố lẻ sao cho
là số nguyên tố lẻ sao cho 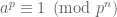 . Chứng minh
. Chứng minh 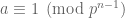 .
.
Lời giải. Theo đề bài ta suy ra 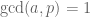 . Áp dụng định lý Fermat nhỏ ta có
. Áp dụng định lý Fermat nhỏ ta có 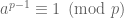 . Do đó
. Do đó 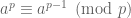 . Mà vì
. Mà vì 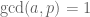 nên
nên 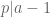 . Ta áp dụng bổ đề LTE thì
. Ta áp dụng bổ đề LTE thì
Vậy 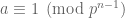 .
.
Ví dụ 3. Giải phương trình nghiệm nguyên dương 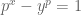 .
.
Lời giải. Với 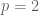 thì phương trình tương đương với
thì phương trình tương đương với 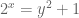 .
.
Nếu 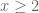 thì
thì 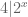 nên
nên 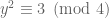 , mâu thuẫn. Vậy
, mâu thuẫn. Vậy 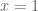 . Khi đó
. Khi đó 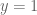 .
.
Với 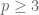 thì
thì 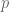 lẻ, phương trình tương đương
lẻ, phương trình tương đương 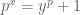 . Ta suy ra
. Ta suy ra 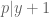 . Áp dụng bổ đề LTE ta có
. Áp dụng bổ đề LTE ta có
Do đó 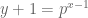 . Với
. Với 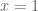 thì
thì 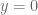 , mâu thuẫn. Vậy
, mâu thuẫn. Vậy 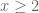 .
.
Ta suy ra 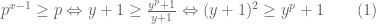 .
.
Tuy nhiên ta lại có 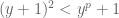 với
với 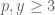 . Vậy nên
. Vậy nên 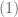 xảy ra khi
xảy ra khi 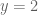 hoặc
hoặc 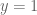 .
.
Với 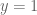 thì
thì 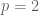 , mâu thuẫn.
, mâu thuẫn.
Với 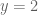 thì
thì 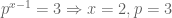 .
.
Vậy phương trình có nghiệm nguyên dương 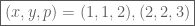
1 comment:
dạ chỗ kia e tưởng phải là 2 mới là số mũ đúng của 5 trong khai triển 5400 chứ ạ
Post a Comment